Friday, 4 November 2016

Digital Image Processing — Image Restoration Models

Unknown 11:46

IMAGE RESTORATION MODELS

The principal goal of restoration technique is to improve an image in some predefined sense. Image restoration is concerned with filtering the observed image to minimize the effect of degradations. Image restoration refers to removal or minimization of known degradations in an image. This includes deblurring of images degraded by the limitation of a sensor or its environment, noise filtering or non-linarities due to sensors.

The fundamental result in filtering theory used commonly for image restoration is called the Wiener filter. This filter gives the best linear mean square estimate of the object from the observation. It can be implemented in frequency domain by the fast unitary transforms.

Other image restoration methods are: - least squares, constrained least squares, and spline interpolation methods. Other methods such as likelihood, maximum entropy, and maximum posteriori are nonlinear techniques that require iterative solutions.

Image Restoration Models: - There are different models of image restoration given below:

1) Image formation models.

2) Detector and recorder.

3) Noise models.

4) Sampled observation models.

5) Detector and Recorder Models.

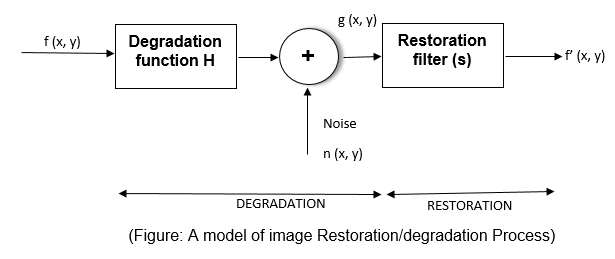
Here, the degradation process is modeled as a degradation function together with an additive noise term, operates on input image f (x, y) to produce a degraded image g (x, y). The restoration approach is based on various types of image restoration filters.

1. Image Formation Model: - The study of image formation encompasses the radiometric and geometric processes by which 2D images of 3D objects are formed. In the case of digital images, the image formation process also includes analog to digital conversion and sampling.

Diffraction-limited coherent systems have the effect of being ideal low-pass filters.

Motion blur occurs when there is relative motion between the object and the camera during exposure. Atmospheric turbulence is due to random variations in the refractive index of medium between the object and the image system. Such degradation occurs in the imaging of astronomical images.

Examples of Spatially Invariant models: -

1) Diffraction limited, coherent (with rectangular aperture)

2) Diffraction limited, incoherent (with rectangular apeture)

3) Horizontal motion

4) Atmospheric turbulence

5) Rectangular scanning aperture

6) CCD interactions

2. Detector and Recorder Model: - The response of image detectors and recorders is generally nonlinear. For example, the response of photographic films, image scanners, and display devices can be written as

g = aw^b

where a and b are device-dependent constant and w is the input variable.

3. Noise Models: - The principal source of noise in digital images arise during image acquisition or transmission. The performance of imaging sensors is affected by a variety of factors, such as environmental conditions during image acquisition, and by the quality of the sensing elements themselves.

For example: In acquiring images with a CCD camera, light levels sensor temperature are major factors affecting the amount of noise in the resulting image.

An image transmitted using a wireless network might be corrupted as a result of lightning or other atmospheric disturbance.

Some important Noise Probability Density Functions: -

1) Gaussian noise: - Because of its mathematical tractability in both the spatial and frequency domains, Gaussian (also called normal) noise model are used frequently in practice. The PDF of a Gaussian random variable, z, is given by:

P(z) = 1 /Ö2πσ x e ^{-(z-z’)/2σ2}

2) Rayleigh Noise

3) Erlang (gamma) Noise

4) Exponential Noise

5) Uniform Noise

6) Impulse (salt-and-pepper) Noise

7) Periodic Noise