Restoration
in The Presence of Noise Only
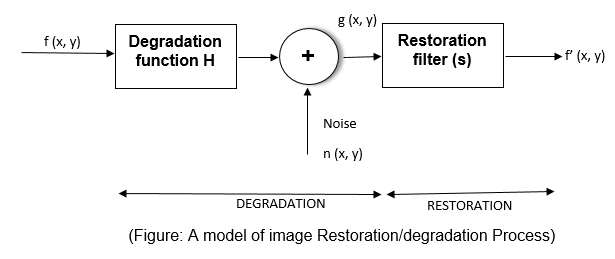
When the only degradation present in an image noise,
equations:
g
(x, y) = f (x, y) + η (x, y)
and
G
(u, v) = F (u, v) + N (u, v)
The noise terms are unknown, so subtracting them from g (x,
y) and G (u, v) is not a realistic option. In this case N (u, v) can be
subtracted from G (u, v) to obtain an estimate N (u, v) from the spectrum of G
(u, v).
Mean
Filters: - The different types of noise reduction mean
filters are given below: -
1.
Arithmetic
Mean Filter: - This is the simplest of the mean filters. Let Sxy
represent the set of coordinates in a rectangular subimage window of
size m x n, centered at a point (x, y). The arithmetic mean filter computes the
average value of the corrupted image g
(x, y) in the area defined by Sxy. The value of the restored image f’
at point (x, y) is simply the arithmetic mean computed using the pixels in the
region defined by Sxy.
f’ (x, y) = 1/mn ∑ g (s, t)
This operation can be
implemented using a spatial filter of size m x n in which all coefficient’s
have value 1/mn. A mean filter smooth local variations in an image and noise is
reduced as a result of blurring.
2.
Geometric
Mean Filter: - An image restored using a geometric mean filter
is given by the expression
f’ (x, y) = [ π(s, t) € Sxy g (s,
t)]
Each restoration pixel is
given by the product of the pixels in the subimage window, raised to the power
1/mn. A geometric mean filter achieves smoothing comparable to the arithmetic
mean filter, but it tends to loss less image detail in the process.
3.
Harmonic
Mean Filter: - Harmonic mean filter works well for salt noise,
but fails for pepper noise. It does well also with other type of noise like
Gaussian noise.
4.
Contraharmonic
Mean Filter: - This filter is well suited for reducing or
virtually eliminating the effects of salt-and-pepper noise.
5.
Median
Filter: -The best known order statistic filter is median filter,
which is as its name implies, replaces the value of pixel by the median of the
intensity levels in the neighborhood of that pixel.
6.
Midpoint
Filter: - The midpoint filter simply computes the midpoint between
maximum and minimum values in the area encompassed by the filter. This filter
combines order statistics and averaging. It works best for randomly distributed
noise, like Gaussian or uniform noise.
7.
Inverse
Filter: - Inverse filtering is the process of recovering the input
of a system from its output. For example, in the absence of noise the inverse
filter would be a system that recovers u (m, n) from the observations v (m, n).
8.
Pseudoinverse
Filer: - It is the stabilized version of the inverse filter.
9.
The
Wiener Filter: - The main disadvantage of inverse filter and
pseudoinverse filter is that these filters remain very sensitive to noise.
Wiener filter is a method of restoring image in the presence of blur as well as
noise.